1. Ntsys Software For Dendrogram Download
2. Ntsys Software For Dendrogram Research
3. Ntsys Software For Dendrogram Visual
4. Ntsys software, free download
5. Ntsys Software For Dendrogram Type

• NTSYSpc is one of the most popular softwares being used in molecular genetic qualitative data cluster analysis. The present paper is showing how we can integrate this powerful software with Microsoft Office Word and Excel in an innovative method to cluster, screen and more varied individuals selection in a populated group studying.
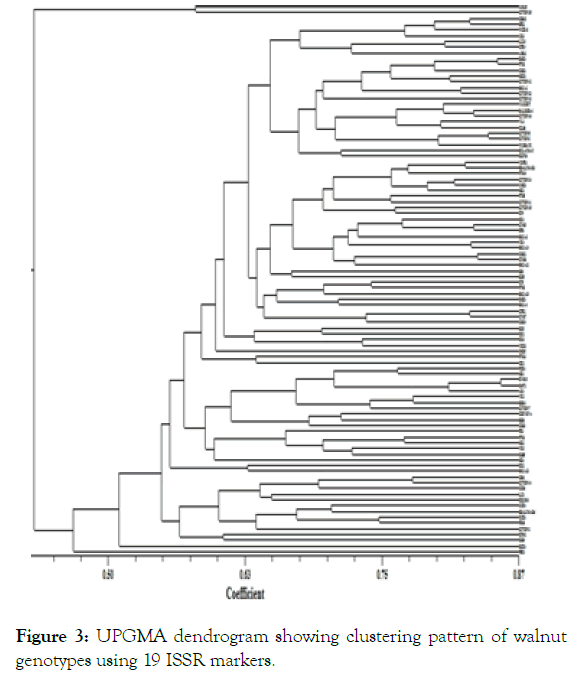
• Based upon the E20 and D18 primer similar as well as maximum polymorphic bands also been observed. Cluster analysis was done based on the UPGMA method using NTSYS software. Dendrogram analysis clearly noticed the Similarity Co-efficient for cultivars in the cluster I, II and II varied from 0.10-0.33, 0.78.

NCSS contains several tools for clustering, including K-Means clustering, fuzzy clustering, and medoid partitioning. Each procedure is easy to use and is validated for accuracy. Use the links below to jump to a clustering topic. To see how these tools can benefit you, we recommend you download and install the free trial of NCSS.

Nihar Ranjan Chattopadhyay, in Induced Fish Breeding, 2017. 10.3.7 Cluster Analysis. UPGMA clustering method was used to generate a dendrogram for the two stocks of C. Catla in Orissa in the present study by computing the GS values with DICE coefficient in NTSYSpc 2.2 program. The dendrogram showed one cluster with the Puri and Ganjam stocks.

Jump to:

Introduction

Clustering or cluster analysis is the process of grouping individuals or items with similar characteristics or similar variable measurements. Various algorithms and visualizations are available in NCSS to aid in the clustering process.

Technical Details

This page provides a general overview of the tools that are available in NCSS for a cluster statistical analysis. If you would like to examine the formulas and technical details relating to a specific NCSS procedure, click on the corresponding ‘[Documentation PDF]’ link under each heading to load the complete procedure documentation. There you will find formulas, references, discussions, and examples or tutorials describing the procedure in detail.

Hierarchical Clustering / Dendrograms

The agglomerative hierarchical clustering algorithms available in this procedure build a cluster hierarchy that is commonly displayed as a tree diagram called a dendrogram. The algorithms begin with each object in a separate cluster. At each step, the two clusters that are most similar are joined into a single new cluster. Once fused, objects are never separated. The eight methods that are available represent eight methods of defining the similarity between clusters.

The eight clustering techniques (linkage types) in this procedure are:

• Single Linkage: Also known as nearest neighbor clustering, this is one of the oldest and most famous of the hierarchical techniques. The distance between two groups is defined as the distance between their two closest members. It often yields clusters in which individuals are added sequentially to a single group.
• Complete Linkage: Also known as furthest neighbor or maximum method, this method defines the distance between two groups as the distance between their two farthest-apart members. This method usually yields clusters that are well separated and compact.
• Simple Average: Also called the weighted pair-group method, this algorithm defines the distance between groups as the average distance between each of the members, weighted so that the two groups have an equal influence on the final result.
• Centroid: Also referred to as the unweighted pair-group centroid method, this method defines the distance between two groups as the distance between their centroids (center of gravity or vector average). The method should only be used with Euclidean distances.
• Median: Also called the weighted pair-group centroid method, this defines the distance between two groups as the weighted distance between their centroids, the weight being proportional to the number of individuals in each group. The method should only be used with Euclidean distances.
• Group Average: Also called the unweighted pair-group method, this is perhaps the most widely used of all the hierarchical cluster techniques. The distance between two groups is defined as the average distance between each of their members.
• Ward’s Minimum Variance: With this method, groups are formed so that the pooled within-group sum of squares is minimized. That is, at each step, the two clusters are fused which result in the least increase in the pooled within-group sum of squares.
• Flexible Strategy: Lance and Williams suggested that a continuum could be made between single and complete linkage. The program also allows you to try various settings of these parameters which do not conform to the constraints suggested by Lance and Williams.

Euclidean or Manhattan distances may be used in these clustering techniques.

Example Dataset of Clustering Data

Example Setup of the Hierarchical Clustering / Dendrograms Procedure

Example Output for the Hierarchical Clustering / Dendrograms Procedure

A Dendrogram from the Hierarchical Clustering / Dendrograms Procedure

K-Means Clustering

The k-means algorithm was developed by J.A. Hartigan and M.A. Wong of Yale University as a partitioning technique. It is most useful for forming a small number of clusters from a large number of observations. It requires variables that are continuous with no outliers.

The objective of this technique is to divide N observations with P dimensions (variables) into K clusters so that the within-cluster sum of squares is minimized. Since the number of possible arrangements is enormous, it is not practical to expect the single best solution. Rather, this algorithm finds a “local” optimum. This is a solution in which no movement of an observation from one cluster to another will reduce the within-cluster sum of squares. The algorithm may be repeated several times with different starting configurations. The optimum of these cluster solutions is then selected.

Some of the reports available in the this procedure include iteration details, cluster means, F-Ratios, distance sections, and bivariate plots.

Some Bivariate Plots from the K-Means Clustering Procedure

Medoid Partitioning

The objective of cluster analysis is to partition a set of objects into two or more clusters such that objects within a cluster are similar and objects in different clusters are dissimilar. The medoid partitioning algorithms available in this procedure attempt to accomplish this by finding a set of representative objects called medoids. The medoid of a cluster is defined as that object for which the average dissimilarity to all other objects in the cluster is minimal. If k clusters are desired, k medoids are found. Once the medoids are found, the data are classified into the cluster of the nearest medoid.

Two algorithms are available in this procedure to perform the clustering. The first, from Spath, uses random starting cluster configurations. The second, from Kaufman and Rousseeuw, makes special use of silhouette statistics to help determine the appropriate number of clusters.

Medoid Algorithm of Spath

This method minimizes an objective function by swapping objects from one cluster to another. Beginning at a random starting configuration, the algorithm proceeds to a local minimum by intelligently moving objects from one cluster to another. When no object moving would result in a reduction of the objective function, the procedure terminates. Unfortunately, this local minimum is not necessarily the global minimum. To overcome this limitation, the program lets you rerun the algorithm using several random starting configurations and the best solution is kept.

Medoid Algorithm of Kaufman and Rousseeuw

Kaufman and Rousseeuw present a medoid algorithm which they call PAM (Partition Around Medoids). This algorithm also attempts to minimize the total distance D (formula given above) between objects within each cluster. The algorithm proceeds through two phases.

In the first phase, a representative set of k objects is found. The first object selected has the shortest distance to all other objects. That is, it is in the center. An addition k-1 objects are selected one at a time in such a manner that at each step, they decrease D as much as possible.

In the second phase, possible alternatives to the k objects selected in phase one are considered in an iterative manner. At each step, the algorithm searches the unselected objects for the one that if exchanged with one of the k selected objects will lower the objective function the most. The exchange is made and the step is repeated. These iterations continue until no exchanges can be found that will lower the objective function.

Note that all potential swaps are considered and that the algorithm does not depend on the order of the objects on the database.

Fuzzy Clustering

Fuzzy clustering generalizes partition clustering methods (such as k-means and medoid) by allowing an individual to be partially classified into more than one cluster. In regular clustering, each individual is a member of only one cluster. Suppose we have K clusters and we define a set of variables that represent the probability that object i is classified into cluster k. In partition clustering algorithms, one of these values will be one and the rest will be zero. This represents the fact that these algorithms classify an individual into one and only one cluster.

In fuzzy clustering, the membership is spread among all clusters. The probability of each object to be in each cluster can now be between zero and one, with the stipulation that the sum of their values is one. We call this a fuzzification of the cluster configuration. It has the advantage that it does not force every object into a specific cluster. It has the disadvantage that there is much more information to be interpreted.

Regression Clustering

The algorithm used in this procedure provides for clustering in the multiple regression setting in which you have a dependent variable Y and one or more independent variables, the X’s. The algorithm partitions the data into two or more clusters and performs an individual multiple regression on the data within each cluster. It is based on an exchange algorithm described in Spath.

Regression Exchange Algorithm

This algorithm is fairly simple to describe. The number of clusters, K, for a given run is fixed. The rows are randomly sorted into the groups to form K initial clusters. An exchange algorithm is applied to this initial configuration which searches for the rows of data that would produce a maximum decrease in a least-squares penalty function (that is, maximizing the increase in R-squared at each step). The algorithm continues until no beneficial exchange of rows can be found.

The following chart shows data that were clustered using this algorithm. Notice how the two clusters actually intersect.

Output from the NCSS Scatter Plot Procedure based on Regression Clustering Procedure Results

Ntsys Software For Dendrogram Download

A dendrogram is a tree diagram often used to demonstrate the arrangement of the clusters produced by hierarchical clustering. Dendrograms are often used in computational biology to illustrate the clustering of genes or samples. As for a dendrogram, each branch is called a clade. The terminal end of each clade is referred to as a leaf. Clades can have only one leaf or many leaves. The arrangement of clades tell us which leaves are most similar to each other.

Edraw includes a full-featured dendrogram solution that can produce high quality full-fledged dendrograms and a lot more types of diagrams. The goal of Edraw is to make drawing/diagramming even easier for both novices and experienced users and everyone in between. It offers an extensive collection of built-in shapes in vector format. Included are tons of interactive tutorial and reference for experienced users, novices, and everyone in between.

Discover why Edraw is an awesome dendrogram maker: Download it Now.

Ntsys Software For Dendrogram Research

Like a race car, there are special features if you want more control over your diagrams.

1. Auto Generation
One click on the floating action button creates another shape automatically. Making dendrogram is easier, faster and funnier than ever before.

2. Quick-start Templates
Included are some dendrogram templates available to Edraw users. They will not only get you going quickly but guide you to create beautifully effective and presentation-quality dendrogram. Our diagramming community keeps adding templates every day. So you're sure to find something suitable to you.

3. All Necessary Symbols
Our object library comes with an awesome set of objects making it super easy to create dendrogram.

4. Linkable Diagrams
The hyperlink function enables you to design dendrograms with working links. That means you can link to web pages or other files from your diagram. This makes it very easy to navigate back and forth between the relevant information. Thus, you can avoid confusion and saves a mass amount of time spent on redoing things.

6. Editable SVG Exports. Works Everywhere.
As a vector-based software, Edraw exports diagrams as SVG documents which can be styled and modified using Vector editors like Adobe Illustrator and Inkscape. The exported editable SVG files are fully fledged documents that can be viewed in any web browser as well as be imported into Microsoft Visio. One file format, infinitely accessible! Great!

Works on Windows 7, 8, 10, XP, Vista and Citrix

Works on 32 and 64 bit Windows

Works on Mac OS X 10.2 or later

Ntsys Software For Dendrogram Visual

Ntsys software, free download

Click the image to download editable dendrogram template and use Edraw to modify it.

1. Product Range Dendrogram

The product range dendrogram template can save many hours in creating great dendrograms by using built-in symbols right next to the canvas. You can click the image download and modify this template for your own use.

2. Animal Kingdom Dendrogram

Ntsys Software For Dendrogram Type

This animal kingdom dendrogram shows classification of animals with two main types, vertebrates and invertebrates.

3. Event Tree Diagram

Here is a event tree diagram which can be downloaded and re-edited to create dendrogram.